高校では習わない逆三角関数。
これは名前の通り二辺の比からなる
直角三角形のなす角度を返す関数です。
突如、説明もなくテキストにこの関数が登場して
何を表しているのか分からない。
理解がそこで止まってしまうことがあります。
逆三角関数をついて授業で教わってるけど
よくわからない。
一体何の役に立つの？
調べてようと思っても
あまり資料がない。
そんな方に向けて
この記事では下記のことを知ることができるわ
- 逆三角関数の定義や公式、性質を一通り復習できる
- 逆三角関数は何の役に立つのか
- どうやって計算すればいいのか
- さらに勉強したい方へのおすすめ教材
ご覧いただく前のご注意点
勾配の角度を知りたい
この標識は山道などでよく見かけます。
意味としては、
この先に勾配9％の下り坂がありますよ
ということをお知らせしています。
勾配10％とは何か？
簡単に説明すると
$$\tan \theta = 0.1$$
という値をとる坂道ですよと示しています。
10%と言われてもよくわからない。
この坂の傾斜はいったい何度なの？
その傾斜の角度を求められる関数が逆三角関数。
定義：逆三角関数とは何か？
動画教材
逆三角関数は初めて聞いた
という方はこちらの動画を紹介。
予備校のノリで学ぶ「大学の数学・物理」
AKITOの勉強チャンネル
Takeaki Yamazaki
定義
この関数の定義は三角関数の逆関数となっています。
$$逆関数：y = f^{-1}(x) \langle x = f(y) \rangle$$
$$y =\arcsin x (x = \sin y) $$
$$y =\arccos x (x = \cos y)$$
$$y =\arctan x (x = \tan y)$$
三角関数の値から角度（ラジアン）を返すという関数です。
例えばsinの値が0.5になる角度はπ/6となりますので
$$\arcsin 0.5 = \frac{\pi}{6}$$
とあらわすことができます。
直角三角形の二辺から角度を求める関数です。
冒頭で述べた勾配の標識についても
$$ \theta = \arctan 0.1 = ?$$
θの値を求めれば、角度が分かります。
紛らわしい書き方
$$\arcsin x = \sin^{-1} x$$
という書き方もあります。
逆関数を
$$f^{-1}(x)$$
と書くことから、このような書き方をするのだと推測されます。
これだと-1乗、つまり\(\frac{1}{sin}\)と言うように勘違いをしやすいわ。
さらに書籍の中には注釈もなく、いきなり書かれています。
私はあまり使いたくはない…
ということでこの記事では
$$\arcsin , \arccos , \arctan$$
という表記で統一します。
基本公式と性質
定義域に注意！
定義域は下記のようになります。
$$\arcsin xの場合は -1 \le x \le 1$$
$$\arccos xの場合は -1 \le x \le 1$$
$$\arctan xの場合は実数全域$$
arcsin、arccosの定義域は
-1~1までしか取れないので注意してください。
sin、cosの値が-1~1の範囲しかとらないので、
逆関数であるarcsin,arccosは-1~1が定義域となります。
主値
\(y=\sin x\)でyが0になるxは無数に存在します。
\( (x= 0,\pm \pi,\pm 2\pi,\cdots)\)のときです。
逆三角関数はこの逆関数なので
例えば\( y = arcsin x\)においてxのある値について
無数のyの値が成り立ちます。
ところがこれだと逆関数の定義上、
全単射にならないので、
そのためにyの値の範囲、すなわち値域の範囲を決める必要があります。
この値域の範囲を「主値」といいます。
主値として下記の区間をとることが一般的です。
$$-\frac{\pi}{2} \le \arcsin x \le \frac{\pi}{2}$$
$$0 \le \arccos x \le \pi$$
$$-\frac{\pi}{2} \le \arcsin x \le \frac{\pi}{2}$$
性質
偶関数、奇関数
$$\arcsin (-x) = -\arcsin x$$
$$\arccos (-x) = \pi -\arccos x$$
$$\arctan (-x) = -\arctan x$$
arcsin,arctanは奇関数になります。
\(\arcsin ,\arccos ,\arctanの関係 \)
下記の三角形を描くと
\(\arcsin ,\arccos ,\arctan \)を
それぞれ簡単に変換できます。
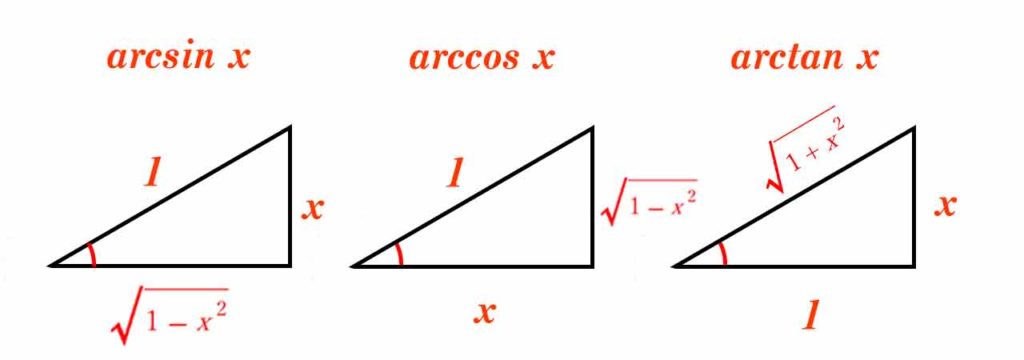
$$\arcsin x = \arccos \sqrt{1-x^2} =\arctan \frac{x}{\sqrt{1-x^2}}(0 < x < 1)$$
$$\arccos x = \arcsin \sqrt{1-x^2} =\arctan \frac{\sqrt{1-x^2}}{x}(0 < x < 1)$$
$$\arctan x = \arcsin \frac{x}{\sqrt{1+x^2}} =\arccos \frac{1}{\sqrt{1-x^2}}(x \ge 0)$$
$$\arcsin x + \arccos x = \frac{\pi}{2}(-1 \le x \le 1)$$
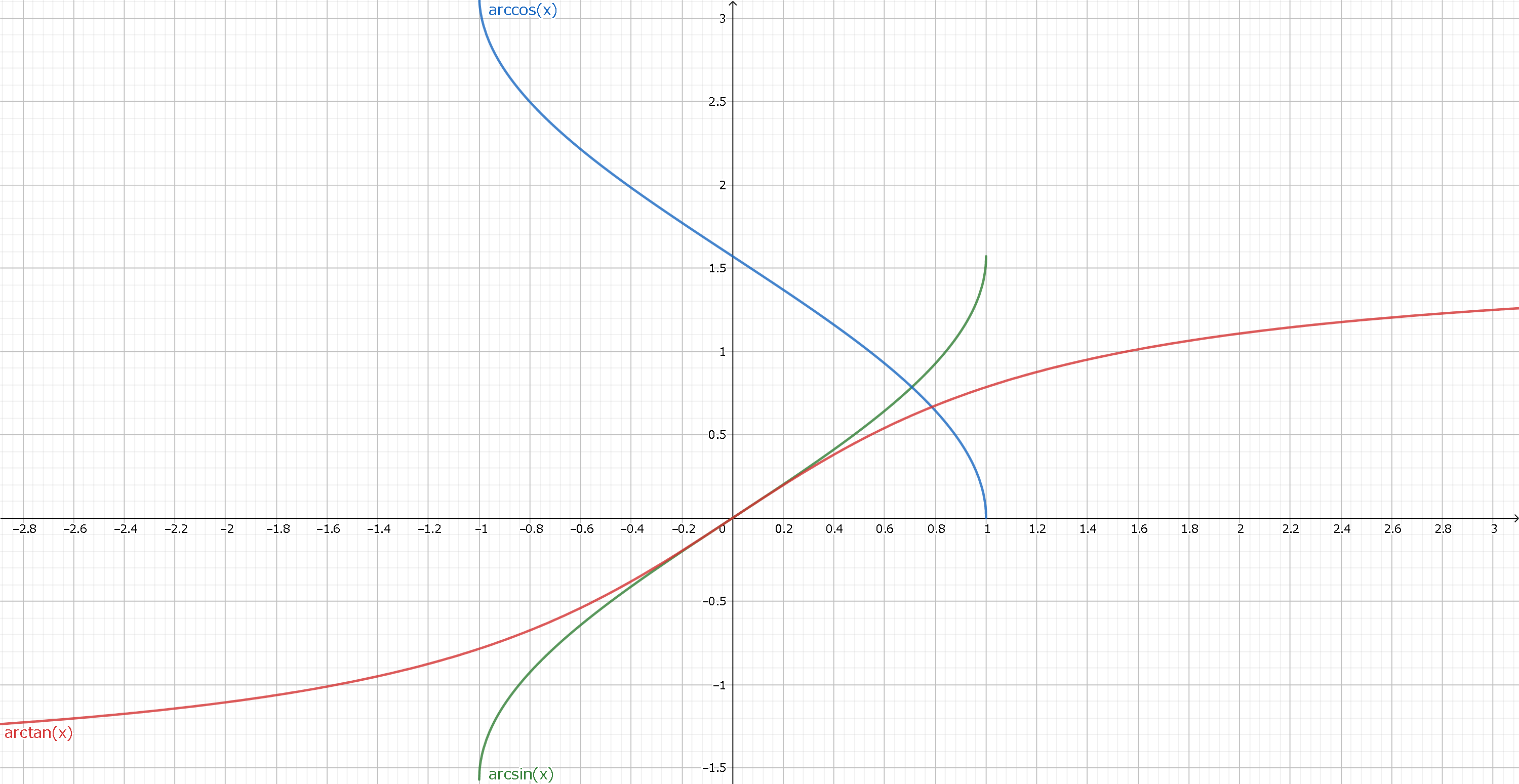
グラフ
y=xを軸にひっくり返せば逆関数のグラフになります。
ただし、主値の項でも説明しましたが、
あるxの値に多数のyの値を対応するわけにはいかないので
実際には主値の範囲である一部分だけを値域とします。
$$緑線 y=\arcsin x\\
青線 y=\arccos x\\
赤線 y=\arctan x$$
微分
$$\frac{d}{dx}\arcsin x = \frac{1}{\sqrt{1-x^2}}$$
$$\frac{d}{dx}\arccos x = -\frac{1}{\sqrt{1-x^2}}$$
$$\frac{d}{dx}\arctan x = \frac{1}{1+x^2}$$
次のような積分もできる
導関数がこのような式になるということは、例えば
$$\int \frac{1}{\sqrt{1-x^2}}dx = -\arccos x +C$$
$$\int \frac{1}{1+x^2}dx = \arcsin x +C$$
と求められます。
積分
$$\int \arccos x dx = x \arccos x – \sqrt{1-x^2} + C$$
$$\int \arctan x dx = x \arctan x – \frac{1}{2}\log(1+x^2) + C$$
arcsin x/x,arccos x/x,arctan x/xのx→0での極限値
有名で重要な極限値
$$\lim_{x\to 0}\frac{\sin x}{x} = 1$$
がありますが、
sinをarcsinにした極限値を求めたらどうなるでしょうか？
結論は下記のようになります。
$$\lim_{x\to 0}\frac{\arccos x}{x} = \pm \infty$$
$$\lim_{x\to 0}\frac{\arctan x}{x} = 1$$
以前$$\lim_{x\to 0}\frac{\arccos x}{x} = 0$$
と書いてしまっていました。
いつの時期か忘れたのですが
実はその間違いに気づき、こっそり修正しています。
arcsin x/xのx→0での極限値
\(t=\arcsin x\)とする。
\(\displaystyle\lim_{x\to 0}\frac{\arcsin x}{x} \\
\displaystyle=\lim_{t\to 0}\frac{t}{\sin t}\\
\displaystyle=\lim_{t\to 0}\frac{1}{\frac{\sin t}{t}} \\
= 1\)
ということで同じ1という値になります。
ということは
$$x\ll 0 ならば \arcsin x \approx x$$
といえます。
arccos x/xのx→0での極限値
\(t=\arccos x\)とする
\(\displaystyle\lim_{x\to 0}\frac{\arccos x}{x} \\
\displaystyle=\lim_{t\to \pi /2}\frac{t}{\cos t} \\
= \pm\infty\)
arctan x/xのx→0での極限値
\(t=\arctan x\)とする。
\(\displaystyle\lim_{t\to 0}\frac{\tan t}{t} = 1\)より
\(\displaystyle\lim_{x\to 0}\frac{\arctan x}{x} \\
\displaystyle=\lim_{t\to 0}\frac{t}{\tan t} \\
\displaystyle=\lim_{t\to 0}\frac{t}{\sin t}\cdot \cos t \\
= 1\)
x\ll 0 ならば \arccos x \approx 0\\
x\ll 0 ならば \arctan x \approx x$$
加法定理
\(\arctan\)については
加法定理が成り立ちます。
ただし\(- \frac{\pi}{2} < \arctan A + \arctan B < \frac{\pi}{2} \)未満。
Machin(マチン)の公式
証明
\(\displaystyle\theta = \arctan \frac{1}{5}とすると\\
\displaystyle\tan \theta =\frac{1}{5}となる。\)
\(\displaystyle\tan 2\theta = \frac{2\tan \theta}{1-\tan^2 \theta}\\
\displaystyle=\frac{2 \times \frac{1}{5}}{1-\frac{1}{25}}=\frac{5}{12}\)
\(\displaystyle\tan 4\theta = \frac{2\tan 2\theta}{1-\tan^2 2\theta}\\
\displaystyle=\frac{2 \times \frac{5}{12}}{1-\frac{25}{144}}=\frac{120}{119}\)
よって
\(\displaystyle\tan (4\theta -\frac{\pi}{4}) = \frac{\tan 4\theta – \tan \frac{\pi}{4}}{1+\tan 4\theta \tan \frac{\pi}{4}}\\
\displaystyle= \frac{\frac{120}{119} – 1}{1+\frac{120}{119} }=\frac{1}{239}\)
よって
\(\displaystyle4\theta -\frac{\pi}{4} = \arctan \frac{1}{239}\\
\displaystyle\frac{\pi}{4} = 4\theta – \arctan \frac{1}{239}\\
\displaystyle=4\arctan \frac{1}{5} – \arctan \frac{1}{239}\)
マクローリン展開
マクローリン展開をすると
arcsin,arccosの式がかなり煩雑になります。
$$\arccos x= \frac{\pi}{2} – \arcsin x=\frac{\pi}{2} -x – \left( \frac{1}{2}\right) \frac{x^3}{3} – \left( \frac{1\cdot 3}{2\cdot 4}\right) \frac{x^5}{5} – \left( \frac{1\cdot 3\cdot 5}{2\cdot 4 \cdot 6}\right) \frac{x^7}{7}-\cdots$$
$$\arctan x= x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\cdots$$
練習問題
arctan x + arctan (1/x) = π/2
\(\arctan x = t \to x = \tan t\)と置いて解く。
どれも同じです。
逆三角関数は三角関数で考える
という問題に行きつくことが多い
\(\lim_{x→0} x \arctan\frac{1}{x}\)
\(\displaystyle\lim_{x\to 0} x\arctan \frac{1}{x} \\
\displaystyle=\lim_{x\to 0} \frac{\arctan \frac{1}{x}}{\frac{1}{x}} = 0\\
(分母が\infty ,分子が\pm \frac{\pi}{2})\)
\(\lim_{x→1}{\frac{1}{x-1}-\frac{1}{\log x}}\)
\(\displaystyle\lim_{x\to 1}{\{ \frac{1}{x-1}-\frac{1}{\log x} \} }\\
\displaystyle=\lim_{x\to 1}\frac{(\log x-x+1)}{(x-1)\log x}\\
\displaystyle=\lim_{x\to 1} \frac{\frac{1}{x}-1}{\log x+1-\frac{1}{x}}(ロピタルの定理より)\\
\displaystyle=\lim_{x\to 1}\frac{-\frac{1}{x^2}}{\frac{1}{x}+\frac{1}{x^2}} (ロピタルの定理より)\\
\displaystyle=-\frac{1}{2}\)
役に立つ範囲は広い
逆三角関数は工学、航法、物理学、幾何学において広く使われる。
Wikipediaより引用
実際はかなりの広範囲です。
特別にここ、というのを探しているのですが
なかなか見つけられずという状況です。
申し訳ありません。
ですが、このように解釈されるといいかと思います。
それは
三角関数が使われるところには
逆三角関数が使われる需要がある
ということです。
三角関数が比の値を返すのに対し、
逆関数である逆三角関数は角度をの値を返します。
三角関数は電気、波、振動など
かなり幅広い分野で使われています。
ということは、同じ頻度で
角度や位相を知りたければ
逆三角関数が使われるので
分野としてはかなり広くなります。
表から見るか
裏から見るか
という違いでしかない
と解釈すれば
それほど悩まなくても済みます。
シューティングゲームのプログラムで、
相手の弾が自機に当たったかどうかを判定するのに
arctanを使うというようなことを聞いたことがあります。
プログラミングの座標上で回転する点の位置を求めるのに
逆三角関数を使うのでプログラミングのコードを書くときには
よく使われるらしい。
工学、航法、物理学、幾何学というすべての分野に
精通しているわけではないけど、
分かり次第、追記していくつもり。
計算するときのポイント
下記の3つを押さえておくといいです。
三角形をイメージ
逆三角関数を使うときは
この図形をイメージしましょう
arcsin と arccos を式変形や関係式を
求めるときにこの図をイメージするとわかりやすいことがあります。
三角関数sin,cos,tanに変換する
arcsin,arccos,arctanは
そのままではあらゆる式変形で扱いづらいので
sin,cos,tanに置き換えて計算します。
微積分では\(1+x^2,1-x^2\)という項が登場する
微積分で$$\sqrt{1-x^2},\sqrt{1+x^2}$$
という項が現れたときには
arcsin,arccos,arctanが出てくるかもしれない
というパターンを頭に入れておくと
手掛かりになることがあります。
具体的な数値計算はExcel、関数電卓で可能
具体的に角度の値を知りたいときは
Excelならasin,acos,atanという関数が用意されています。
また関数電卓にも$$\sin^{-1} ,\cos^{-1} ,\tan^{-1}$$
という表記のボタンがあるのが一般的なので
そこから計算できます。
またこちらのサイトからも計算ができます。
まとめ
勾配の標識ですが、
10%の場合は何度なのか確認しました。
| 関数名 | 値（度） | 値（度分秒） |
| atan(x) | 5.7105931374996 | 5°42′38.14″ |
こちらのサイトで値を計算しました。
約6度です。
スキー場の初級者コースが10度ぐらいなので、それよりもゆるい傾斜です。
思ったほど急な傾斜でもないですね。
逆正弦法則
関連するツイート
逆三角関数関連のツイートもまとめてみました。
— 微咲&素々奈&証莉＠数学関連 (@misa_suzu_aka) July 20, 2022