高校の数学ではsin,cos,tan という奇妙な表記が出てきます。
ですが、決して難しくありません。
角度を入力すると、斜辺と底辺の比を出力するというだけです。
これらを三角関数と呼びます。
三角関数は辺の長さを求める以外にも色んな便利な用途があります。
この記事では三角関数の定義からその公式、応用をまとめています。
高校の数学で登場する”sin,cos,tan”という文字
高校の数学で突如出てくる
$$\sin \theta,\cos \theta,\tan \theta$$
いったいこれは何なのか?
これを使うとどんな便利なことがあるのか?
中学の数学でxやyが登場して
それまでの小学校の算数とは別世界に来たことで
面食らってしまうことがありますが、
高校の数学では
$$\sin x,\cos x,\tan x$$
などという奇妙な表記が出てきます。
まるで中学の数学で面食らったときのように
高校の数学で面食らってしまう方も多いと思います。
$$\sin x,\cos x,\tan x$$
というのは難しい話ではありません。
\(x\)という角度に対して、斜辺と底辺の比を
これらの記号であらわしているにすぎません。
ひとかたまりで捉えていただけるとわかりやすいです。
これらを三角関数と呼びます。
ところが、この三角関数は辺の長さを求める以外にも
色んな便利な用途があることがわかってきました。
そのためか三角形の比の値という枠を超えて
いろんな分野で利用されています。
ご覧いただく前のご注意点
三角関数の定義
a:対辺、b:底辺、c:斜辺とすると、
$$\cos \theta = \frac{b}{c}$$
$$\tan \theta = \frac{a}{b}$$
実はほかにも
$$\sec \theta(=\frac{1}{\cos \theta}) , \csc \theta(=\frac{1}{\sin \theta}) , \cot \theta(=\frac{1}{\tan \theta})$$
もありますが、いまではほとんど使われません。
逆数に変換するだけなので
$$\sin,\cos,\tan$$
に直してしまえばOKです。
そもそもなんで使うようになった?(推測)
これがあると何が便利かというと
例えば木の高さhを図りたいときに、
ある点と木との距離d、木のテッペンとある点がなす角度a
が分かってさえいれば、木の高さが
$$h = \tan a$$
で求められることです。
つまり角度と一辺がわかれば他辺の長さが計算できるからです。
昔は角度と比の値の一覧表があって、
角度が何度かわかれば、三角形の一辺にその値をかけることで
高さが求められます。
キャラ設定-icon.jpg)
同じように川の幅も測れたりできるわけです。
三角関数基本公式まとめ
三角関数の公式は覚えないと、
試験問題を解けないことが多いです。
キャラ設定-icon.jpg)
覚えることがどうしても嫌な人は
公式の導き方を頭に入れておくことでもOKです。
キャラ設定-icon.jpg)
そちらの方が応用が利くこともあったりします。
暗記すべき角度と三角比
以下の値は覚えましょう。
0度、30度、45度、60度、90度の場合は
九九と同じでスラスラと出ないと
計算が厳しいです。
キャラ設定-icon.jpg)
三角定規を思い浮かべながら覚えよう。
(三角定規は30度、60度、90度と45度、45度、90度の2種類です。)
$$\sin 0^\circ=0,\cos 0^\circ = 1,\tan 0^\circ = 0$$
$$\sin 30^\circ=\frac{1}{2},\cos 30^\circ = \frac{\sqrt{3}}{2},\tan 30^\circ = \frac{1}{\sqrt{3}}$$
$$\sin 45^\circ=\frac{1}{\sqrt{2}},\cos 45^\circ = \frac{1}{\sqrt{2}},\tan 45^\circ = 1$$
$$\sin 60^\circ=\frac{\sqrt{3}}{2},\cos 60^\circ = \frac{1}{2},\tan 60^\circ = \sqrt{3}$$
$$\sin 90^\circ=1,\cos 90^\circ = 0$$
0度の三角形?三角比がマイナスになる?
0度の三角形?というのは実際には存在しません。
ですが、0度の三角関数の値を定義すると便利なことが多いです。
今までは三角形を使って説明をしていましたが、
半径1の正円を使って説明すると三角関数がより広く便利に利用できます。
分かりやすい動画がこちらになります。
キャラ設定-icon.jpg)
三角形の各辺の比からできたので三角関数という名前にしたと思うけど、
「円関数」という名前にした方が分かりやすかったかも。
それぐらい「円」と深いかかわりがあります。
弧度法の導入
角度の単位は度数法といって
360度を1回転とする表記を使っていましたが、
高校数学では、弧度法という角度の単位を使っています。
単位の名前はラジアン(rad)です。
- \(2\pi\)で1周
- 半径と同じ円弧の長さとなる角度を1(rad)
最初はちょっとピンと来ないかもしれませんが、
使っていくうちに慣れます。
$$0^\circ = 0 (rad) , 30^\circ = \frac{\pi}{6} (rad) , 45^\circ = \frac{\pi}{4} (rad)$$
計算上、こちらのほうが絶対的に便利であるため、
高校数学からはこちらを使います。
正弦定理
Rは三角形に外接する円の半径です。
余弦定理
$$b^2 = c^2 + a^2 -2ca\cos B$$
$$c^2 = a^2 + b^2 -2ab\cos C$$
直角(角度が90度)のときはcosの値が0になるので、
ピタゴラスの定理と同じ式になります。
つまり、ピタゴラスの定理を拡大したのが余弦定理
という言い方もできるわけです。
三角形の面積
2辺と1つの角度が分かれば三角形の面積も
簡単に求められます。
簡単な性質
$$\cos (-\theta) = \cos \theta$$
$$\tan (-\theta) = -\tan \theta$$
sinとtanは奇関数、cosは偶関数です。
加法定理
キャラ設定-icon.jpg)
加法定理は導出するよりも暗記したほうが早いかな。
キャラ設定-icon.jpg)
時間短縮ですよ。
$$\sin (\alpha – \beta)=\sin \alpha \cos \beta – \cos \alpha \sin \beta$$
$$\cos (\alpha + \beta)=\cos \alpha \cos \beta – \sin \alpha \sin \beta$$
$$\cos (\alpha – \beta)=\cos \alpha \cos \beta + \sin \alpha \sin \beta$$
$$\tan (\alpha + \beta)=\frac{\tan \alpha + \tan \beta}{1-\tan\alpha\tan\beta}$$
$$\tan (\alpha – \beta)=\frac{\tan \alpha – \tan \beta}{1+\tan\alpha\tan\beta}$$
積→和の公式
積から和の公式は暗記してもOKですし、
上記の式を足して2で割る、引いて2で割るでも出てくるので、
自分で導いてもいいです。
$$\sin \alpha \sin \beta = \frac{1}{2}\{\cos (\alpha – \beta)-\cos (\alpha + \beta)\}$$
$$\cos \alpha \cos \beta = \frac{1}{2}\{\cos (\alpha + \beta)+\cos (\alpha – \beta)\}$$
キャラ設定-icon.jpg)
2倍角、3倍角も覚えちゃった方が早い。
$$\cos 2\alpha = \cos^2 \alpha -\sin^2 \alpha$$
$$=2\cos^2 \alpha -1$$
$$=1-2\sin^2 \alpha$$
$$\sin 3\alpha = 3\sin \alpha – 4\sin^3 \alpha$$
$$\cos 3\alpha = 4\cos^3 \alpha – 3\cos \alpha$$
積分するときに出てきますので、
できるようにしておきましょう。
和→積の公式
キャラ設定-icon.jpg)
加法定理から導出するのもOK。
簡単に導けます。
$$\sin A – \sin B = 2\cos \frac{A+B}{2} \sin \frac{A-B}{2}$$
$$\cos A + \cos B = 2\cos \frac{A+B}{2} \cos \frac{A-B}{2}$$
$$\cos A – \cos B = -2\sin \frac{A+B}{2} \sin \frac{A-B}{2}$$
グラフ
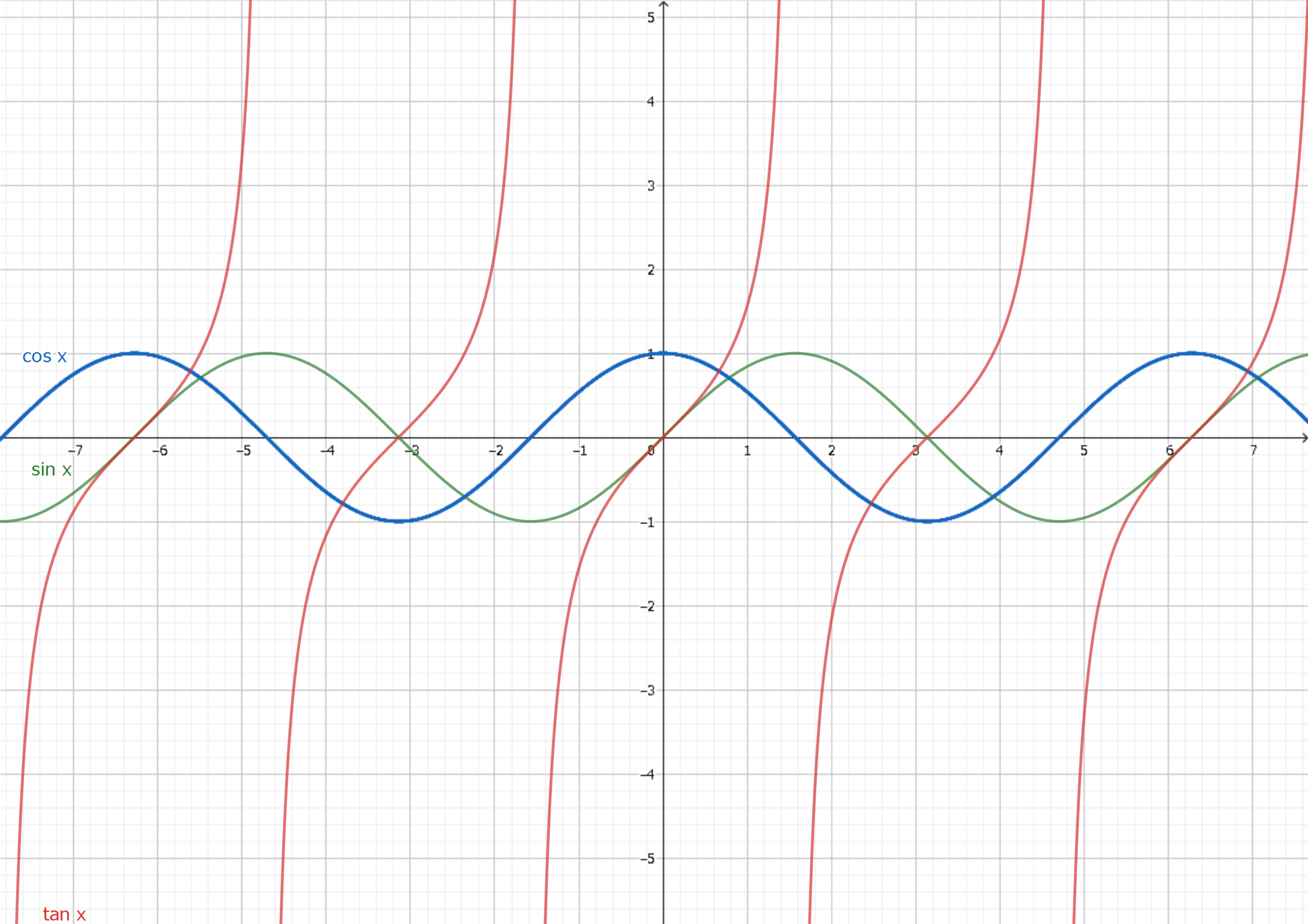
sinとcosはグラフを描くと、「波」の形になります。
そして(π/2だけ)横にずれているだけで形が同じ
ということもわかります。
ということは実質的にsinとcosは同じようなグループという認識ができます。
半径1の正円を原点に中心をおいて書いたとき、
円周上に点のx座標がcos、y座標がsinの値となります。
tanのグラフは特筆するところはあまりないです。
tanは「傾き」と覚えておきましょう。
\(\frac{\pi}{2}\)に近づくにつれて無限大に飛んでいきます。
漸近線が\(x=\frac{\pi}{2}+n\pi(n:整数)\)で発生します。
sin x/xのx→0の極限値
この式は超重要です。
$$\lim_{x\to 0} \frac{\sin x}{x} = 1$$
式を覚えると同時に、
どのような意味があるのか?
何に応用が利くのか?
を理解するとよくわかります。
微分
微分は次のような式になりますが、
注意しなくてはならないのは角度は弧度法(ラジアン)となっています。
度数法だと\( \pi / 180 \)が係数としてついてしまいます。
$$\frac{d}{dx}\cos x= -\sin x$$
$$\frac{d}{dx}\tan x= \frac{1}{\cos^2 x}$$
積分
微分の時と同様に角度はラジアンです。
$$\int \cos x dx = \sin x +C$$
$$\int \tan x dx = -\log_e | \cos x | +C$$
オイラーの公式
これが超重要です。
$$e^{i\theta} = \cos \theta + i \sin \theta$$
過去の入試問題を解いてみる
鈴木貫太郎さんの動画にもいっぱい紹介されています。
4倍角の式も、加法定理もしくはド・モアブルの定理を使えば式変形できます。
あとは定義域に注意して、最大値、最小値を求められます。
下記の記事で問題の解法を紹介しています。
再生リストのまとめ
応用分野
物理の「力学」で使われる三角関数
例えば重力を2方向に分離するときに使われます。
角度が分かるだけでいいので非常に便利です。
高1の物理の最初の方で出てくるので、
数学の授業よりも先に登場して、

なんじゃこれは!
とざわついてしまうこともありますが、
全く難しいことはないです。
物理の「単振動」「波動」
物理の「単振動」「波動」はまさしく正弦波、三角関数をそのまま使う分野ですので
密接に関係しています。
波の基本式として、そのまま出てきます。
$$y = A \sin \frac{2\pi}{T}(t-\frac{x}{v})$$
$$A:振幅,T:周期,t;時間,x:位置,v:波の速さ$$
物理の「交流回路」
交流回路も三角関数の理解が不可欠です。
電圧を次のようにした電気回路をつくります。
$$V = V_0 \sin \omega t$$
ちなみに電流値はつぎのようになります。
$$I = I_0 \sin \omega t$$
こうするといろいろと便利なことが出てくるんです。
コイルとコンデンサーと抵抗を組み合わせた回路の問題につながっていきます。
雑学
動画で学びたい方はこちらの教材
余弦定理から数学的センスが分かる⁈
この余弦定理の式を暗記するだけではなく、
ちゃんと意味が分かっているか、
三角形の性質を理解した応用した考え方ができるか
ということを数学的センスとして説明しています。
計算を間違えないように少しでも工夫するという姿勢は大事です。
大学数学で使われる三角関数
テイラー展開
【1年前の今日】
— ヨビノリやす (@Yasu_Yobinori) July 22, 2018
1年前の今日公開した動画
《テイラー展開の気持ち》
まだ活動を始めたばかりの頃の動画ですが、今でも人気のある動画のひとつです!まだ見たことない人はぜひチェックを!https://t.co/p7Rnf9eVhj pic.twitter.com/82Wv0zkYCu
三角関数を多項式に近似することができます。
フーリエ級数展開
【新着動画】どの分野でも必ずと言っていいほど現れる「フーリエ変換」の気持ちを解説しました。この単元ほど”気持ち”の理解が重要であるものが浮かびません
— ヨビノリたくみ😬 (@Yobinori) April 8, 2018
賛否両論のボケ(×2)が収録されています。あなたはどのような評価を下しますか?https://t.co/JQ5RRcMHNA pic.twitter.com/U4lTpbgts4
あらゆる関数を、sinの関数の多項式で近似するのがフーリエ級数展開です。
キャラ設定-icon.jpg)
テイラー展開の三角関数版というざっくりとした認識でもOK。
複素関数としての三角関数
定義域を複素数つまり
$$\sin(x + iy)$$
という三角関数に複素数を代入したらどうなるか?
ということを考える分野もあります。
複素数まで考えると、
$$\sin z = 2$$
という方程式も実数解はないですが、
複素数解なら存在します。
三角関数に関連する関数
逆三角関数
逆三角関数という名前の通り二辺の比の値から角度を返す関数。
プログラミングなどの分野でも応用される関数。
加法定理など類似した公式がある
双曲線関数
双曲線関数の定義自体はネイピア数を使った関数だが、
成り立つ公式が三角関数に酷似している。
まとめ
想像以上に奥が深いというか、
この関数を起点にいろんな分野で使われている印象です。
正弦波は電気回路で作りやすい、
正弦波は波紋のように実生活で見たことある形、
というのが大きいのかなと思います。
さらに深く勉強したい方は動画だけでなく
本での勉強もおすすめです。





