・#AmongUs で二回インポスター、そのうち2回負ける。
・#factorio を一瞬
・プログラミング言語「Gamin(仮名)」の開発を再開
・逆三角関数を勉強。ただし、普通の三角関数より難しく、理解できなかった。誰か、逆三角関数を説明できる方がおりましたら教えて欲しいです。
— waryu_YND (@waryu_ynd) September 16, 2021
逆三角関数という関数があります。
高校数学で必須ではないですが、
知っているといろいろと便利な関数です。
この記事では
逆三角関数の積分を求めます。
基本的には逆三角関数を三角関数に変換して
そこから積分をして、また変数を
元の逆三角関数に戻すだけです。
難しくないことがわかります。
ご覧いただく前のご注意点
逆三角関数の積分
$$\int \arccos x dx = x \arccos x – \sqrt{1-x^2} + C$$
$$\int \arctan x dx = x \arctan x – \frac{1}{2}\log(1+x^2) + C$$
証明
\(\arcsin x = t \to x = \sin t\\
\arccos x = t \to x = \cos t\\
\arctan x = t \to x = \tan t\)
と置きかえる。
そのままでは扱いづらいので
\( \sin,\cos,\tan \)に置き換えて計算します。
キャラ設定-icon.jpg)
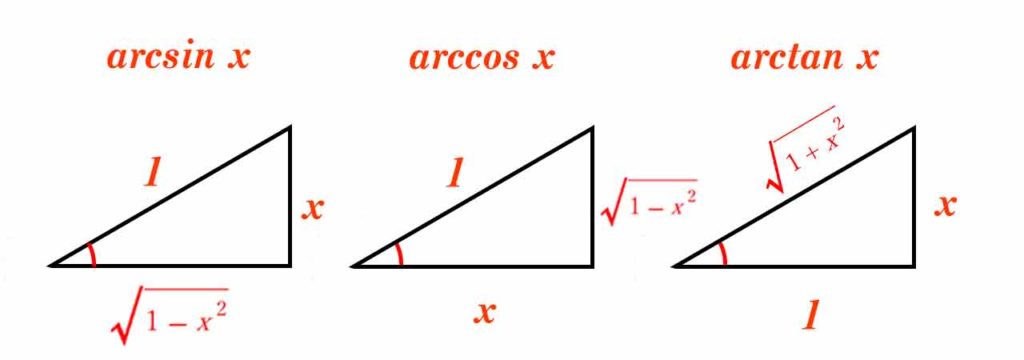
この置き換えをまずは考えてみる。
arcsinの積分
\(\arcsin x = t \to x = \sin t\)
と置き換えて計算します。
このとき
\(dx = \cos t dt\)
となるので
\(\displaystyle\int \arcsin x dx \\
=\displaystyle\int t \cos t dt\\
=t \sin t – \int 1 \cdot \sin t dt\\
=t \sin t + \cos t + C\\
=t \sin t + \sqrt{1-\sin^2 t} + C\\
= x \arcsin x + \sqrt{1-x^2} + C\)
arccosの積分
\(\arccos x = t \to x = \cos t\)
と置き換えて計算します。
このとき
\(dx = – \sin t dt\)
となるので
\(\displaystyle\int \arccos x dx \\
=\displaystyle-\int t \sin t dt\\
=t \cos t – \int 1 \cdot \cos t dt\\
=t \cos t – \sin t + C\\
=t \cos t – \sqrt{1-\cos^2 t} + C\\
= x \arccos x – \sqrt{1-x^2} + C\)
arctanの積分
\(\arctan x = t \to x = \tan t\)
と置き換えて計算します。
このとき
\(\displaystyle dx = \frac{1}{\cos^2 t} dt\)
となるので
\(\displaystyle\int \arctan x dx \\
=\displaystyle\int \frac{t}{\cos^2 t} dt\\
=t \tan t – \int 1 \cdot \tan t dt\\
=t \tan t +\log |\cos t| + C\\
=t \tan t +\log \frac{1}{\sqrt{1+\tan^2 t}} + C\\
=x \arctan x + \log \frac{1}{\sqrt{1+x^2}} + C\\
=x \arctan x – \frac{1}{2}\log (1+x^2) + C\)
キャラ設定-icon.jpg)
想像するほど、難しくはない。


