【sinh,conh,tanh】双曲線関数の公式一覧【三角関数と類似する関数】

大学数学の参考書で双曲線関数という
関数が登場します。

$\sinh ,\cosh ,\tanh$という三角関数のような記号を
使って表します。。

定義を見ると$e^xとe^{-x}$の式です。
この関数を見ると大きな疑問が浮かびます。

なぜ三角関数のような記号を割り当てているのか？
なぜ双曲線関数という名前を付けたのか？

そのような疑問に答えるため
この記事では双曲線関数の
特徴や性質、公式をまとめています。

基本公式や性質
まとめ

ご覧いただく前のご注意点

数学

「数学」の記事一覧です。

当方の学習した内容を
理解し伝えることを目的としていますが
説明に脆弱な点や
表記に誤記がある場合がございますので
あらかじめご了承ください。
随時、修正していきます。

基本公式や性質

定義

【新着動画】「双曲線関数とは何か」大学数学で突如現れる双曲線関数を基本から解説。『ハイパボリックサインシータ』、言うだけで頭が良くなった気がします

受験数学では背景知識までおさえて挑みたいという活気に満ちた高校生にもおすすめですhttps://t.co/w1yaHpKzuC pic.twitter.com/JVjNHWf3hO
— ヨビノリたくみ😬 (@Yobinori) October 14, 2017

双曲線関数を次のように定義します。

$$\sinh x =\frac{e^x – e^{-x}}{2}$$
$$\cosh x =\frac{e^x + e^{-x}}{2}$$
$$\tanh x =\frac{e^x – e^{-x}}{e^x + e^{-x}}$$

素々奈（すずな）

三角関数みたいね

読み方

それぞれ

ハイパボリックサイン$\sinh $
ハイパボリックコサイン$\cosh $
ハイパボリックタンジェント$\tanh $

と読みます。

ハイパボリックhyperbolicとは日本語で「双曲線」のことを言います。

証莉（あかり）

なぜ、双曲線と名付けたのか？
なぜ、三角関数のような記号を割り当てたのか？

この疑問に答えていきます。

基本公式

三角関数のような記号を使う理由

見ての通り三角関数の表記にhを付け足しただけです。
それは三角関数に似ている性質があるからです。

$\sin,\cos,\tan $の公式と
$\sinh,\cosh,\tanh $の公式が
とても似ています。

三角関数と類似する最重要公式

まずは定義から次の式が成り立ちます。

$$\tanh x = \frac{\sinh x}{\cosh x} $$

$\displaystyle\tan x = \frac{\sin x}{\cos x} $という式と類似しています。

$\cos^2 x + \sin^2 x=1$という
三角関数でよく使われる公式が
双曲線関数ではこのようになります。

$$\cosh^2 x – \sinh^2 x =1 $$

（証明）
$$\cosh^2 x = (\frac{e^x+e^{-x}}{2})^2\
=\frac{e^2x +2+ e^{-2}}{4}$$$$\sinh^2 x = (\frac{e^x-e^{-x}}{2})^2\
=\frac{e^2x -2+ e^{-2}}{4}$$よって
$$\cosh^2 x – \sinh^2 x\
=\frac{e^2x +2+ e^{-2}}{4} – \frac{e^2x -2+ e^{-2}}{4}\
=1$$<

両辺を$ \cosh x $で割ると次のようになります。

$$1 – \tanh^2 x =\frac{1}{\cosh^2 x} $$

これも三角関数の
$\displaystyle 1+\tan^2 x =\frac{1}{\cos^2 x} $という式と
類似しています。

微咲（みさき）

三角関数と並列に扱えそうだね。
いろいろと都合が良さそうなのが分かる。

この他にも微分や加法定理など
三角関数と類似している性質が多くあります。
注意する点は符号が異なる点です。
混同しないように注意が必要です。

双曲線関数と呼ばれる理由

$\cosh^2 x – \sinh^2 x =1 $この公式が

$x^2 -y^2 =1$という双曲線の式と
同じ形になることから、
そのように名付けられたと推測されます。

$(x,y)=(\cosh \theta , \sinh \theta )$という
媒介変数表示が可能です。

ちなみに三角関数の場合は
$(x,y)=(\cos \theta , \sin \theta )$と置くことで
$\cos^2 x + \sin^2 x =1$という式が成り立ちます。

双曲線関数の微分

微分すると次のようになります。

$$(\sinh x)’ = \cosh x$$
$$(\cosh x)’ = \sinh x$$
$$(\tanh x)’ = \frac{1}{\cosh^2 x}$$

（証明）
$$\begin{align}
(\sinh x)’ &= (\frac{e^x – e^{-x}}{2})’\\
&=\frac{e^x + e^{-x}}{2}\\
&=\cosh x
\end{align}
$$
$$(\cosh x)’ = (\frac{e^x + e^{-x}}{2})’\\
=\frac{e^x – e^{-x}}{2}\\
=\sinh x$$$$(\tanh x)’ = (\frac{\sinh x}{\cosh x})’\\
=\frac{\cosh^2 x – \sinh^2 x}{\cosh^2 x}\\
=\frac{1}{\cosh^2 x}$$

これも三角関数の微分と似ています。
$$(\sin x)’ = \cos x\\
(\cos x)’ = -\sin x\\
(\tan x)’ = \frac{1}{\cos^2 x}$$
ただし$\cosh$の微分だけ符号が異なります。

双曲線関数の積分

三角関数の微分とほぼ一緒です。

$$\int \sinh x dx = \cosh x +C$$
$$\int \cosh x dx = \sinh x +C$$
$$\int \tanh x dx = \ln|\cosh x| +C$$

加法定理

$$\sinh(x+y) = \sinh x \cosh y + \cosh x \sinh y\\
\sinh(x-y) = \sinh x \cosh y – \cosh x \sinh y\\
\cosh (x+y)=\cosh x\cosh y+\sinh x\sinh y\\
\cosh (x+y)=\cosh x\cosh y-\sinh x\sinh y\\
\tanh (x+y)=\frac{\tanh x+\tanh y}{1+\tanh x\tanh y}\\
\tanh (x-y)=\frac{\tanh x-\tanh y}{1-\tanh x\tanh y}$$

これも三角関数の加法定理とほぼ同じ。
ただしcoshの符号だけ注意。

グラフ

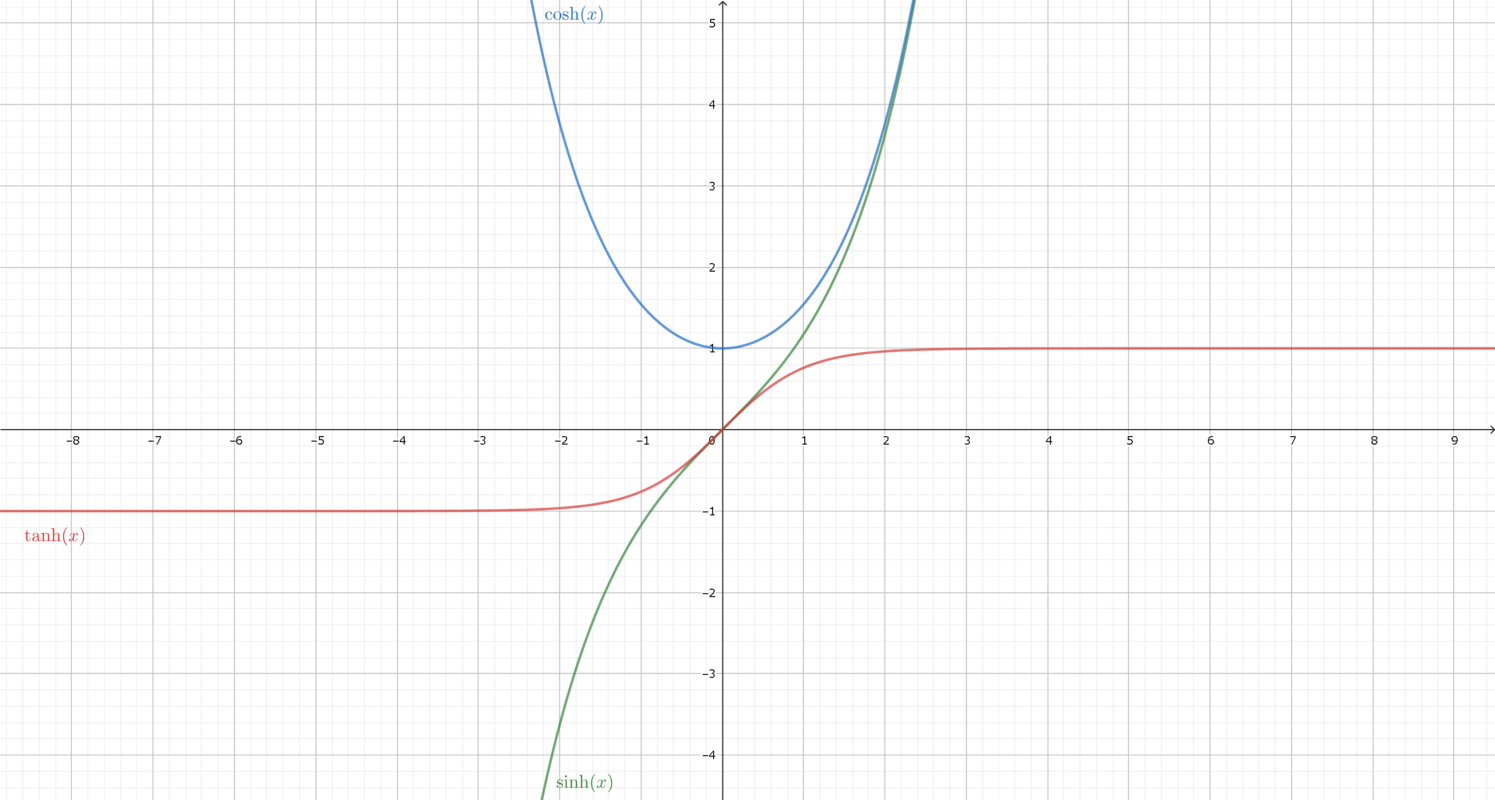
グラフは下記のようになります。

$\sinh x$：緑
$\cosh x$：青
$\tanh x$：赤

懸垂線

$\cosh $は日常生活でも見られる曲線です。
両端にロープをもって垂らすと
このような曲線になることが知られています。
この曲線の名前を「懸垂線」といいます。

証莉（あかり）

他にも電線やネックレスがたるんだ時の曲線の形も
この懸垂線となります。

微咲（みさき）

こんな複雑な関数で表現されていたんだね

テイラー展開

$x=0$で多項式近似をすると

$$
\begin{align}
&\cosh x=1+\frac{x^{2}}{2!}+\frac{x^{4}}{4!}+\frac{x^{6}}{6!}+\cdots \\
&\sinh x=x+\frac{x^{3}}{3!}+\frac{x^{5}}{5!}+\frac{x^{7}}{7!}+\cdots \\
&\tanh x=x-\frac{x^{3}}{3}+\frac{2}{15}x^{5}-\frac{17}{315}x^{7}+\cdots
\end{align}
$$

双曲線関数を虚数範囲に拡張すると三角関数に変換される

双曲線関数に虚数を代入すると次の式が成り立ちます。

$$\sinh i\theta =i \sin \theta \\
\cosh i\theta = \cos \theta$$

(証明)
こちらのオイラーの公式より
$$e^{i\theta}= \cos \theta +i \sin \theta\\
e^{-i\theta}= \cos \theta -i \sin \theta$$この二式から次が成り立ちます。$$\sin \theta= \frac{e^{i\theta}-e^{-i\theta}}{2i} = \frac{1}{i}\sinh i\theta$$
$$\cos \theta= \frac{e^{i\theta}+e^{-i\theta}}{2} = \cosh i\theta$$

つまり、双曲線関数に虚数を代入したものが三角関数になります。

また、三角関数に虚数を代入した場合を考えます。

$$\sin i\theta= i\sinh \theta\\
\cos i\theta= \cosh \theta$$

(証明)
$$\sin i\theta= \frac{1}{i} \sinh (i\cdot i\theta)\\
= -i\sinh (-\theta) = i\sinh \theta \\
\cos i\theta= \cosh (i\cdot i\theta) \\
= \cosh (-\theta) = \cosh \theta$$

三角関数に虚数を代入した値が
双曲線関数に実数を代入した値に対応しています。

複素数に範囲を広げる

双曲線関数に複素数を代入する場合を考えてみます。

複素数$x + iy$のときに次の式が成り立ちます。

$$\sinh (x+iy) = \frac{e^{x+iy}-e^{-x-iy}}{2} = \sinh x \cos y + i \cosh x \sin y\\
\sinh (x-iy) = \frac{e^{x-iy}-e^{-x+iy}}{2} = \sinh x \cos y – i \cosh x \sin y\\
\cosh (x+iy)= \frac{e^{x+iy}+e^{-x-iy}}{2} = \cosh x\cos y + i \sinh x \sin y\\
\cosh (x-iy)= \frac{e^{x-iy}+e^{-x+iy}}{2} = \cosh x\cos y – i \sinh x \sin y\\
\tanh(x+iy)= \frac{\tanh x + i\tan y}{1+i\tanh x \tan y}\\
\tanh(x-iy)=\frac{\tanh x – i\tan y}{1-i\tanh x \tan y}$$

(証明)
$$\sinh (x+iy) = \frac{e^{x+iy}-e^{-x-iy}}{2} \\
=\frac{e^x e^{iy} -e^{-x}e^{-iy}}{2}\\
=\frac{e^x (\cos y + i \sin y)-e^{-x}(\cos y -i \sin y)}{2}\\
=\frac{(e^x -e^{-x})\cos y +i(e^x +e^{-x})\sin y}{2}\\
=\frac{e^x -e^{-x}}{2}\cos y+i \frac{e^x +e^{-x}}{2}\sin y
= \sinh x \cos y + i \cosh x \sin y$$$$\sinh (x-iy) = \frac{e^{x-iy}-e^{-x+iy}}{2} \\
= \sinh x \cos y – i \cosh x \sin y$$$$\cosh (x+iy)= \frac{e^{x+iy}+e^{-x-iy}}{2} \\
=\frac{e^x e^{iy} +e^{-x}e^{-iy}}{2}\\
=\frac{e^x (\cos y + i \sin y)+e^{-x}(\cos y -i \sin y)}{2}\\
=\frac{(e^x +e^{-x})\cos y +i(e^x -e^{-x})\sin y}{2}\\
=\frac{e^x +e^{-x}}{2}\cos y+i \frac{e^x -e^{-x}}{2}\sin y\\
= \cosh x\cos y + i \sinh x \sin y$$$$\cosh (x-iy)= \frac{e^{x-iy}+e^{-x+iy}}{2} \\
= \cosh x\cos y – i \sinh x \sin y$$$$\tanh(x+iy)= \frac{\sinh (x+iy)}{\cosh (x+iy)}\\
=\frac{\sinh x \cos y + i \cosh x \sin y}{\cosh x\cos y + i \sinh x \sin y}\\
=\frac{\tanh x + i\tan y}{1+i\tanh x \tan y}$$$\tan $は奇関数より
$$\tanh(x-iy)=\frac{\tanh x – i\tan y}{1-i\tanh x \tan y}$$

双曲線関数の定義域を複素数に広げると、
三角関数と双曲線関数の積を足した式になります。

証莉（あかり）

三角関数の定義域を虚数にすることで
双曲線関数とのつながりがあることがわかるわ